Q.1 The bending moment, M, of a beam of length l is given by:
dM/dx = w(x+1),
where w is the load constant. If M(0) = 0, find M as a function of x
Q.2 Solve the following separable differential equations:
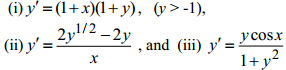
Q.3. Solve the following initial value problem:
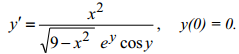
Q. 4.Which of the following differential equations is exact:
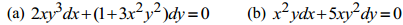
Find the solution of the exact differential equation.
Q.5 Solve the following differential equation with the given initial value.
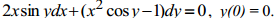
Q. 6. The differential equation : P(x,y)dx + Q(x,y)dy = 0 is not exact. However, if it is multiplied by an integrating factor F(x), it can be made exact. Show that the integrating factor F(x) is given by the solution of the following differential equation:
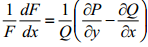
Q.7. First find the integrating factor of the following differential equation and then find its general solution:
2coshxcos ydx = sinh xsin ydy
Q. 8. The following ODEs are in the form of y' + p(x)y = r(x), find their solutions.
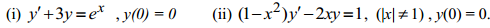
Q.9. Find a homogeneous second order linear ODE of the form of :
