problem1) Which of the following statements are true? Give reasons for your answer.

i) If A and B are similar matrices, they must be congruent.

ii) If A is a positive definite matrix, then so is  A^-1

iii) If A and B are n X n similar matrices, then they have the same eigenspaces.

iv) If T is a diagonalisable linear operator, then the geometric multiplicity of each of its eigenvalues is 1.

v) If T has a unique Jordan form J, then J must be a diagonal matrix.

vi) The spectral radius of a square matrix has to be a positive real number.

vii) ∃ A ∈ M₃ (C) such that A is not triangulisable.

viii) If the row sum of a square matrix A is d, then d is an eigenvalue of A.

ix) If B is the Moore-Penrose inverse of A, then A is t he Moore-Penrose inverse of B.

problem2a) Let T:C³→ C³ T: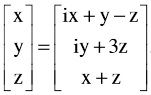 Fin[T]_B, [T]_B'and P , where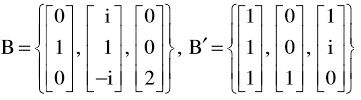

b) If C and D are n × n matrices such that CD =- DC  and D^-1exists, then show that  C is  similar to -C. Hence show that the eigenvalues of C must come in plus-minus pairs. Further, give an ex of a square matrix A which is not similar to –A.

c) Can A be similar to A+I? Give reasons for your answer.

problem3)a) Let T: R³→ R³: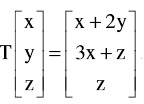. Obtain the generalised eigenspaces of T of orders 2 and 3, for each eigenvalue of T. 

b) Find the possible Jordan forms of B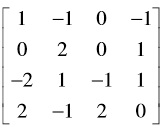

c) Let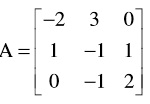. Find an invertible matrix P so that P^-1 AP  is in block diagonal form.