Task 1

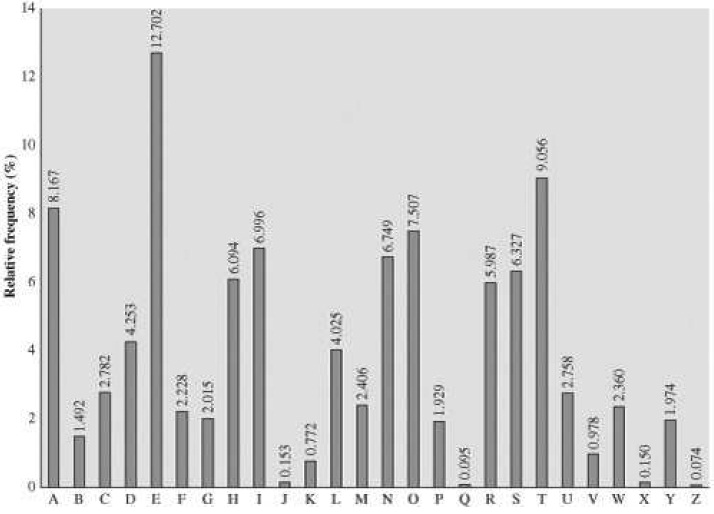
a. Consider the table in Figure given below showing the relative frequencies of letters in English. Arrange the frequencies from largest to smallest, and make a cumulative plot, using Excel for ex. Which smallest group of letters accounts for at least 50% of all letters used in English?

Requirements:

Include all steps to reach the solution as a clear, well-labelled graph and correct answer to letter set

b. An affine cipher scheme can be mathematically expressed in the following form

 C(x) = (αx +β) mod 26.

Here α and β  are numbers selected in the range 1 ≤ α , β < 26, and x represents a letter converted to a number using the rule a = 0,  b = 1,…,   y = 24 and z = 25.

i. What are the α and β  values for the Caesar cipher? Show the steps and solution

ii. Encrypt the plaintext “MOUNTPANORAMA” using  α = 11 and  β = 7.
Show the solution plus the transformed alphabet

iii. Why is  α = 2 and  β = 0 not a good choice of affine cipher parameters when there are 26 letters in the alphabet?
Provide a convincing argument supported by worked ex

c. An affine cipher does not alter the letter frequencies of the plaintext, but merely rearranges them. Describe a general method for recovering α and β  from the two most frequent letters observed in a large amount of ciphertext.

Presentation of the argument or proof, using equations, to recover the affine cipher parameters and the use of a supporting ex

Task 2

a. The keyspace for a cipher is the set all of possible keys that can be used for the cipher. A DES key consists of 56 (independent) bits.

i. Express the size of the DES keyspace to the nearest power of 10, and find three exs of physical quantities, or other known values, that are approximately the same size.

Correct power of 10, and 3 exs with evidence of correctness

ii. Consider the collection of passwords defined by combinations of digits and letters (both upper and lower case). What password length would be required so that the number of possible passwords is at least the size of the DES keyspace? Correct password length with working solution

b. Encryption is only useful if there is a matching reversible operation called decryption. In a Feistel cipher, the F-function or round function need not be reversible.

i. Show that F-function of DES is not reversible

Provide an ex showing that part of all of the DES round function cannot be reversible

ii. describe how a Feistel cipher whose main component is not reversible can actually support decryption.

Provide a correct written description supported by diagram

Task 3

a. Let DES_k(P) denote the DES encryption of the plaintext P by the key K.

i. If we set K to be the key consisting of all zeroes, describe why encrypting twice with this key for DES has the same effect as encrypting then decrypting. Equivalently, account for the following property when using the all-zero key:

 DES_k(DES_k(P)) = P

Provide correct argument involving interaction of key schedule, encryption and decryption of DES

ii. Find another key that also has this property, and describe the structure of the DES key schedule that permit such keys to exist.

Provide the correct identification of the additional key and a convincing explanation of the DES key schedule property that produces equivalent keys for encryption and decryption

b. Let  denote the complement of a sequence of bits, so that for ex 0100 = 1011. Then considering the round structure of DES, show that

DES_k(P) =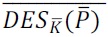 

In other words, complementing the key, plaintext and ciphertext produces the same ciphertext as when none of these values is complemented.

Hint: Use the following property of the XOR function X ⊕ X  = 0. Provide a correct argument for describeing the reason for the complementation in DES, using diagrams involving the round function

Task 4

a. The basis of differential cryptanalysis is finding a pair of differences (ΔP ,ΔC  ) such that plaintext pairs whose XOR difference is ΔP lead to a corresponding ciphertext difference ΔC  after a certain number of rounds. The pair (ΔP ,ΔC ) is called a differential.

The figure below shows a 64-bit differential for DES, which can be written in hexadecimal as:

ΔP = ΔC  = 40 08 00 00 04 00 00 00

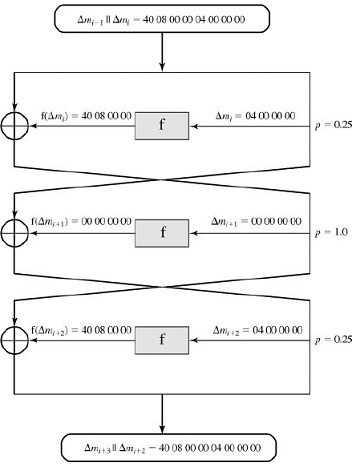
This differential predicts the difference of ciphertexts after 3 rounds with a probability of

1/4 x1x1/4=1/2²

i. How many plaintext pairs of difference ΔP need to be considered by an attacker on average before ΔC is observed as the difference between the ciphertexts after 3 rounds? Hint: How many times on average must you flip a coin before seeing a head? Correct answer with working shown

ii. The differential in the figure above has the property that ΔP = ΔC  after three rounds, and is called iterative since it can be joined to itself to create a differential for a larger number of rounds. What is the probability of this differential if it is extended out to 15 rounds? Correct answer with working shown

iii. The data complexity of a differential attack is the number of pairs needed to recover information about the key. Show that if the attack is using a differential with probability " then the data complexity must be at least 1/p pairs. Correct answer with working shown

iv. Consider a version of DES extended out to 64 rounds, using the same Ffunction, and consider an attack using the iterative differential described in this task. At what round would the data complexity of the attack exceed the amount of available plaintext? Correct answer with working shown.