problem1)
a) Make truth table for
i) p→(~q ? ~ r) ? ~p ? q
ii) ~p→~r ? q ? ~p ? r
b) If A = {1, 2, 3, 4, 5,6,7,8, 9} B = {2, 3, 5, 6, 7} Then find A Δ B .
c) prepare down appropriate mathematical statement which could be represented by following symbolic properties.
i) (∀ x) (∀y) (∃ z) P
ii) ∀(x) (∃y) (∃z) P
problem 2)
a) Define proof? Describe how direct proof is different from indirect proof. Describe method of direct proof with the help of an ex.
b) Show if √11 is rational or irrational.
c) Consider a set X = [2, 3, 4) and the Relation defined on X by.
R = {(2, 2) (2, 3) (3, 3) (3, 4) (2, 4) (4, 4)}. Find whether R is :
i) Reflexive
ii) Symmetric
iii) Transitive
Also justify your answer.
problem 3:
a) Survey among students of college. 60 Study Hindi, 40 study Spanish, and 45 study Japanese, Further 20 study Hindi and Spanish, 25 study Hindi and Japanese, 15 study Spanish and Japanese and 8 study all the languages. Determine the followings:
i) How many students are studying at least one language?
ii) How many students are studying only Hindi?
iii) How many students are studying only Japanese?
b) If p and q are statements, show if the statement [(~p→q) ? (~q)] → (~p ? ~q) is a tautology or not.
problem 4:
a) Make logic circuit for the following Boolean expressions:
i) (x′ ? y ? z) + (x ? y ? z)′
ii) ( x' ? y) ? (y′ ? z) ? (y ? z′)
iii) (x ? y) ? (y ? z)
b) Describe principle of duality. Determine dual of Boolean expression of the output of the following logic circuit:
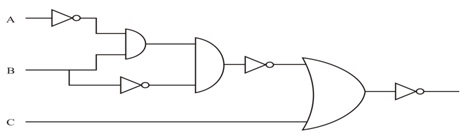
c) Set A,B and C are:
A = {1, 2, 4, 5,6,19}, B = { 1,2,5,22, 44 } and C { 2, 5,11,19,25,40}, Find A ∩ B ∪ C and A ∪ B ∪ C.
problem 5:
a) Draw the Venn diagram to represent following:
i) (A Δ B) ∩ (C~B)
ii) (A ∪ B) ∩ (B Δ C)
b) describe relation mathematically. Also give at least two ex of relations.
c) Show that n3 + 2n is divisible by 3 for all n≥ 1 by induction.
problem 6:
a) Describe inclusion-exclusion principle? Also describe one application of inclusion-exclusion principle.
b) If f : R → R is a function such that f (x) = 3x + 5, prove that f is one - one onto. Also determine the inverse of f.
problem 7:
a) Find how many 3 digit numbers are even? How many 3 digit numbers are composed of odd digits?
b) How many different 15 persons committees could be formed each containing at least 4 Project Managers and at least 3 Programmers from the set of 10 Project Managers and 10 Programmers?
c) Assume we have ten rooms and want to allot five of them to five programmers as offices and use remaining five rooms for computer terminals. Describe in how many ways this could be done.
problem 8:
a) describe Demorgan’s Law? Describe use of Demorgan’s law with an ex.
b) Two dice, one red and one white are rolled. What is the probability that the white die turns up a smaller number than the red die ?
c) Describe pigeon hole principle. Using this principle demonstrate that in any group of 36 people, we could always find 6 people who were born on the same day of week.