Answer all the problems. 

problem1) Construct one Turing Machine for computing each of the following functions

(i)  f (m, n) = m*n, where ‘*’ denotes multiplication

(ii) f (m, n) =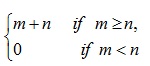

problem2) Construct one grammer for each of the following languages

(a) {a^mbⁿ: m

(b) {w ∈ {0,1}* w=w^R}    

problem3) Show that each of the following functions is primitive recursive:

(i)  f (m, n)   = 4mn

(ii) f (m, n)   = (5n)^2m

problem4) Define following concepts formally:

a) Kleene Closure of an alphabet set.

b) Finite Automata

c) Godel Number

d) Regular Expression

e) Primitive Recursive Function

f) Unsolvable Problem

g) Turing-Decidable Problem

h) Moore Automata

problem5) (i)  Construct the DFA (Deterministic Finite Automata) accepting following Set:

{w ∈ {a,b}*: w has the even number of a’s and odd number of b’s}    

(ii) Construct Turing Machine for the following languages:

1) {aⁿbⁿcⁿ : n > 1}

2)  ww^R : w is any string of 0’s and 1’s}