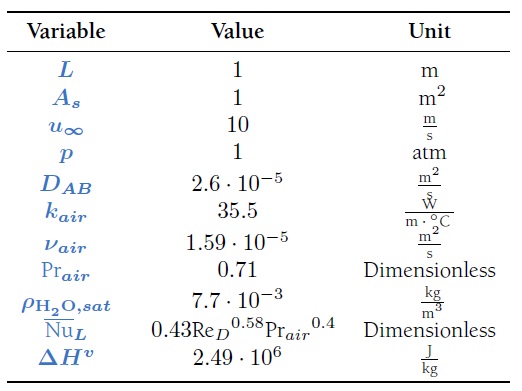
Problem1) Consider the temperature distribution in a 1D flat plate, insulated at x = L and exposed to convective heat transfer at x = 0. On the axes below, sketch what the distribution looks like for the semi-infinite slab solution, the truncated exact solution, and the exact solution for the indicated value of the Fourier number.

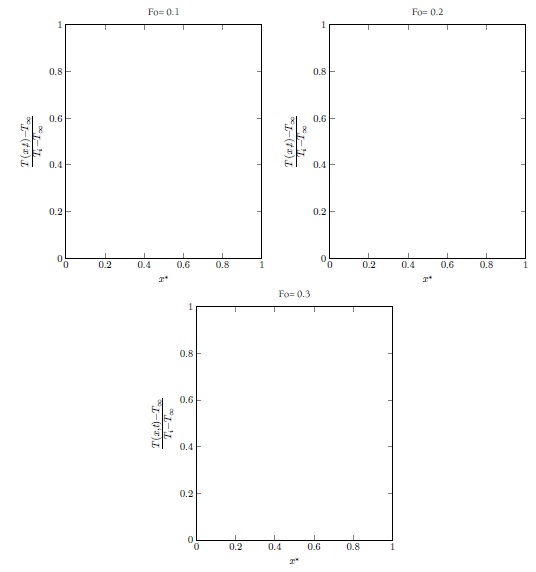
Problem 2 Consider the 2D shape below. Draw a possible configuration of nodes and cells (at least 15) that could be used to solve for the temperature distribution. Provide equations that would be used to solve for the transient temperature distribution using the implicit method for a corner node, a left edge node, and a right edge node.

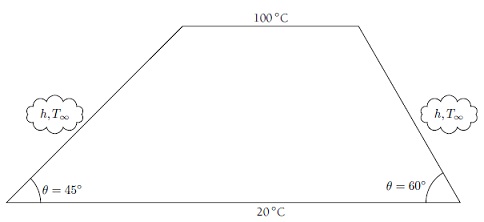
Problem 3a) Show that the Nusselt number for a sphere in a quiescent fluid is 2. Hint: prepare the thermal resistance for the outer surface of the sphere in terms as both conductive and convective resistances, and then equate the two.

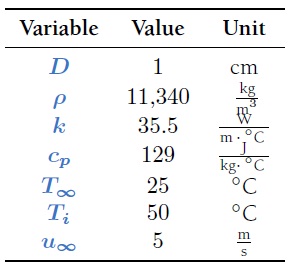
Problem 3b) Ranz and Marshall recommended the correlation NuD‾ = 2 + 0.6Re_D^1/2Pr^1/3 for a lead sphere with D = 1cm in a constant applied flow. If the air speed is u_∞= 5m/s , what is the surface temperature of the sphere at Fo= 1?

Problem4) Consider laminar flow through two infinitely wide parallel plates spaced D apart from one another. What is the thermal entry length?

Problem5) On a summer day the air temperature is 27^°C and the relative humidity is 30%. Water evaporates from the surface of a lake at a rate of 0.10 kg/h per square meter of water surface area. The temperature of the water is also 27^°C. Determine the value of the convection mass transfer coefficient.

Problem6) An industrial process involves the evaporation of water from a liquid film that forms on a contoured surface. Dry air is passed over the surface, and from laboratory measurements the convection heat transfer correlation is of the form appearing in the table below. What is the evaporation rate if the air has the properties listed below?