problem 1: Consider a heat-exchanger control loop with no dead time. It is controlled by a PD controller. The rate time is 0.25 min. A real PD controller is used with filtering where α = 0.1.
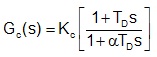
The heat exchanger control loop has the following transfer function (time constants in seconds)
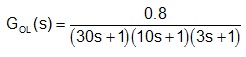
Determine the maximum gain of the system Kcu. What are the corresponding GM & PM if we set Kc = Kcu/1.7.
problem 2: Consider the previous heat exchanger. Tune a proportional controller for
a) GM = 2; PM = 45 degrees and
b) MPH (maximum peak height) occurs at 2 dB (provides a ς of ~ 0.4).
problem 3: Consider the following transfer functions. Neatly sketch their Bode plots and compare with the Matlab figures.
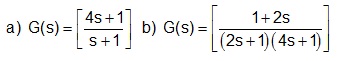
problem 4: Consider the cascade loop as shown below:
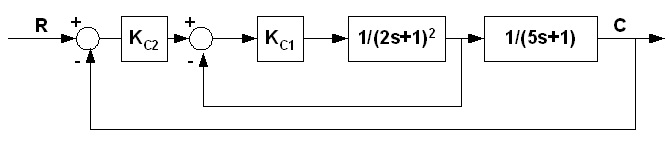
i) Specify the inner-loop gain such that the damping coefficient of the closed loop is equal to 0.4
ii) Derive the ultimate primary controller gain.
iii) Deduce the ultimate gain for the system configured as a conventional loop.
