problem 1: n vehicles occupy squares (1, 1) through (n, 1) (i.e., the bottom row) of an n × n grid. The vehicles must be moved to the top row but in reverse order; so the vehicle i that starts in (i, 1) must end up in (n - i + 1, n). On each time step, every one of the n vehicles can move one square up, down, left, or right, or stay put; but if a vehicle stays put, one other adjacent vehicle (but not more than one) can hop over it. Two vehicles cannot occupy the same square.

a) find out the size of the state space as a function of n.

b) find out the branching factor as a function of n.

c) Suppose that vehicle i is at (x_i, y_i); prepare a nontrivial admissible heuristic hi for the number of moves it will require to get to its goal location (n - i + 1, n), assuming no other vehicles are on the grid. Give a formula for hi in terms of x_i, y_i, and n.

d) Which of the following heuristics are admissible for the problem of moving all n vehicles to their destinations? describe.

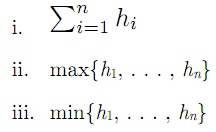
problem 2: Describe the search algorithm that results from each of the following special cases. How does it relate to other algorithms we have discussed.

a) Local beam search with k = 1.

b) Local beam search with one initial state and no limit on the number of states retained.

c) Simulated annealing with T = 0 at all times (and omitting the termination test).

d) Simulated annealing with T = ∞ at all times.

e) Genetic algorithm with population size N = 1.