problem 1: Melissa Bakery is preparing for the coming thanksgiving festival. The bakery plans to bake and sell its favorite cookies; butter cookies, chocolate cookies and almond cookies. A kilogram of butter cookies needs three cups of flour, one cup each of special ingredient and choc chip. A cup of special ingredient is added to five cups of flour altogether with three cups of choc chic to bake a kilogram of chocolate cookies. For baking a kilogram of almond cookies; Melissa needs four cups of flour, a cup of special ingredient and two cups of choc chip. Though, each day the bakery can only allocate at most 400 cups of flour, 100 cups of special ingredient and 210 cups of choc chip to bake the cookies. Melissa estimates a daily profit of RM10 for butter cookies, RM20 for chocolate cookies and RM15 for almond cookies. The bakery wishes to maximize the daily profit.

a) Formulate the given dilemma as a linear programming problem.

b) The given is the final simplex tableau for the above problem:

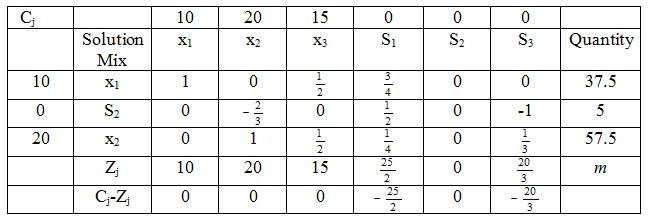
•    Set up the initial simplex tableau for the above problem.             
•    How many kilograms of each cookie should be baked?
•    Find out the value of m?                   
•    Identify any ingredient which is not fully utilized. State the amount unused.
•    How would the optimum solution change if the RHS value for the first resource rises by 10 units?

problem 2: The Maju Supermarket stocks Munchies Cereal. Demand for Munchies is 4,000 boxes per year and the super market is open all through the year. Each box costs $4 and it costs the store $60 per order of Munchies, and it costs $0.80 per box per year to keep the cereal in stock. Once an order for Munchies is placed, it takes 4 days to receive the order from a food distributor.

a) Find out the optimal order quantity.           
b) Find out the total inventory cost related with the optimal order quantity.
c) What is the reorder point?                   
d) What is the cycle time?

problem 3:

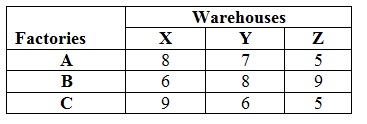
a) A company has three factories A, B and C which supply units to warehouses X, Y and Z every month. The capacities of the factories are 60, 70 and 80 units at A, B and C correspondingly. The requirements of X, Y and Z per month are 50, 80 and 80 units correspondingly. Transportation costs per unit in ringgits are provided in the given table. How many units must ship from each factory so that the total cost is minimum? Use VAM technique for the initial solution and Stepping Stone method to get an optimal solution.

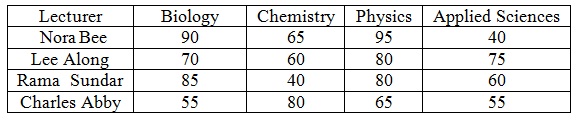
b) The Dean of the Faculty of Science at City Science University has decided to apply the Hungarian method in assigning lecturers to courses for the next semester. As a criterion for judging who must teach each course, the Dean reviews the past two years teaching evaluations (which were filled out by students). As each of the four lecturers taught each of the four courses at one time or another throughout the two-year period, the Dean is able to record a course rating for each lecturer. These ratings are described in the table below. Find the best assignment of lecturers to courses to maximize the on the whole teaching rating.

problem 4: The project of building a backyard swimming pool comprises of eight main activities and has to be completed within19 weeks. The activities and related data are given in the table shown below:

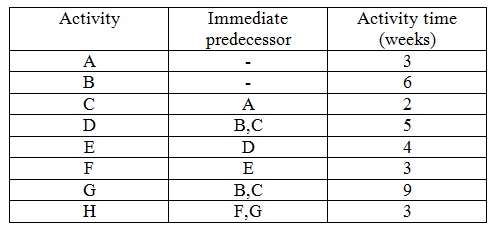
a) Draw a network diagram for this problem.
b) Find out the critical path and the expected project completion time.