problem 1) John, a retired government officer, has recently received his retirement benefits, viz., provident fund, gratuity, etc. He is contemplating as to how much funds he should invest in various alternatives open to him so as to maximize the return on investment. The investment alternatives are – government securities, fixed – deposits of a public limited companies, equity shares, time deposits in a bank, and a house construction. He has made a subjective estimate if the risk involved on a five – point scale. The data on return on investment, the number of years fir which the funds will be blocked to earn this return on investment and the subjective risk involved are as follows:

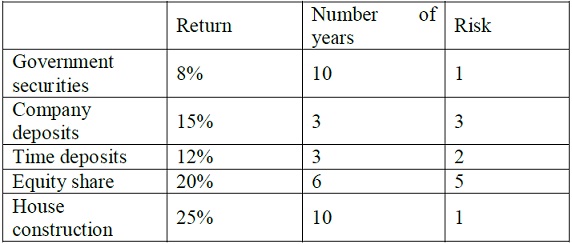
He was wondering what percentage of funds he should invest in each alternative so as to maximize the return on investment. He decided that the average risk should not be more than 3, and the funds should not be locked up for more than 10 years. He would necessarily invest at 25% in house construction. Formulate the linear programming problem.

(B) Solve the game shown below by L.P method.

              B1            B2           B3
A1         6             -1               5
A2         4              0              -4
A3         1             7               10

problem 2)(A) Solve the linear programming problem using the two phase method.

Minimize Z = 2x₁ + x₂
Subject to 5x₁ + 10x₂ – x₃ =8
x₁ + x₂ + x₄ =1
x₁ x₂, x₃, x₄ ≥ 0

(B) In 18th century, when transportation systems were not developed, a family wanted to travel from their home to reach a friend’s home in other part of the country. They had a choice of alternate routes and haltages between their home and the destination. The costs of travel from each point to the other point on route, based on such factors as distance, difficulty, mode of transportation, etc are given below.

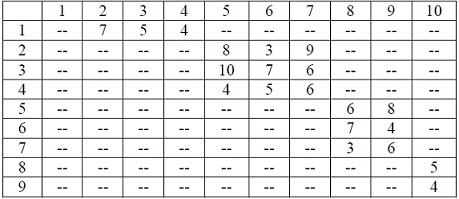
Find the safest route so that the total travelling cost is minimum. Use forward and backward recursion.

problem 3)(A)Use the dual simplex method to solve

Minimize Z = 3x₁ + x₂
Subject to 3x₁ + x₂ ≥ 4
x₁ – x₂  ≥ 0
x₁, x₂ ≥ 0

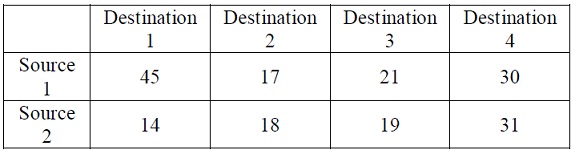
(B) A car rental company is faced with an allocation problem resulting from rental agreements that allow cars to be returned to locations other than those at which they were originally rented. At the present time, there are two locations (sources) with 15 and 13 surplus cars, respectively, and four locations (destinations) requiring 9, 6, 7 and 9 cars, respectively. Unit transportation costs (in dollars) between the locations are as follows: