problem 1: A store is known for is bargains. The store has the habit of lowering the price of its bargains each day, to make surethat articles are sold fast. Suppose that you spot an item on Wednesday (there is only one of it left) that costs 30 Euro and that you would like to buy for a friend as present for Saturday. You know that the price will be lowered to 25 Euro on Thursday when the item is not sold, and to l0 Euro on Friday. You estimate that the probability that the item will be available on Thursday equals 0.7. You further estimate that supposing that it is still available on Friday when it was available on Thursday equals 0.6. You are sure that the item will no longer be available on Saturday. When you postpone your decision to buy the item to either Thursday or Friday, and the item is sold, you will buy another item of 40 Euro as present for Saturday.

a) Formulate the problem as stochastic dynamic programming problem. Specify phases, states, decisions and the optimal value function.

b) Draw the decision tree for this problem.

c) Give the recurrence relations for the optimal value function.

d) What is the minimal expected amount which you will pay for your present, and what is the optimal decision on Wednesday?

problem 2: G. Ambler has € 10000 available for a second hand car, but would like to buy a fast car that costs € 25000. He requires the money for that car quickly, and would like to raise his capital to € 25000 via a gambling game. To this end, he can play a game in which he is allowed to toss an imperfect (with probability 0.4 for heads) coin three times. For each toss he might bet each amount (in multiples of € 1000 and the amount should be in his possession). He will win the amount (that is, receives twice the amount of the bet) when he tosses head, and loses his betted amount when he tosses tails. Use stochastic dynamic programming to find out a strategy which maximises the probability of reaching € 25000 after three tosses.

a) Find out the phases n, states i, decisions d, en optimal valuefunction f_n(i) for this stochastic dynamic programming problem.
b) Give the recurrence relations for the optimal value function.
c) Find out the optimal policy, and describe in words what this policy does. What is the expected probability of succes?

problem 3: Each day you own 0 or 1 stocks of certain commodity. The price of the stock is a stochastic process which can be modeled as a Markov chain with transition rates as follows:

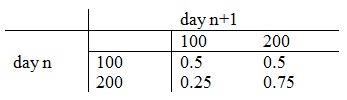
At the beginning of a day at which you own a stock you may select to either sell at the current price, or keep the stock. At the beginning of a day at which you do not own stock, you might select to either buy one stock at the current price or do nothing. You have initial capital of 200.

Your target is to maximize the discounted value of the profit over an infinite horizon, use discountfactor 0.8 (per day).

a) Define the states and give for each state the possible decisions.
b) Formulate the optimality equations.
c) Carry out two iterations of value iteration.
d) Formulate the L.P.-model to solve this problem. describe how you can obtain the optimal policy from the LP formulation.
e) Select a stationary policy and investigate by using the policy iteration algorithm whether or not that policy is optimal.
f) Give the number of stationary policies. Motivate your answer using the definition of stationary policy.

problem 4: The supply of a certain good is inspected periodically. If an order is placed of size x > 0 (integer), the ordering costs are 8 + 2.x. The delivery time is zero. The demand is stochastic and equals 1 or 2 with probability 1/2. Demand in subsequent periods are independent. The size of an order must be such that (a) demand in a period is always satisfied, and (b) the stock at the end of a period never surpasses 2. The holding costs in a period are 2 per unit remaining at the end of a period. Target is to minimize the expected discounted costs over infinite horizon, use discount factor 0.8.

a) Give the optimality equations for the Markov decision problem.
b) Give an LP-model that allows you to find out the optimal policy.
c) Carry out two iterations of the value iteration algorithm
d) Select an odering policy, and investigate using the policy iteration algorithm whether or not this policy is optimal.

problem 5: Customers arrive to a super market according to a Poisson process with intensity ς = 1/2 per minute. The supermarket has two counters, which use a common queue. Counter 1 is always occupied. Counter 2 is opened when 3 or more customers are in the queue, and will be closed when the counter becomes idle (no customer is served at counter 2). The service time of a customer has an exponential distribution with mean 1/Ω = 1 minute.

a) Draw the transition diagram for this queueing system. describe the states, transitions and transition rates.
b) Give the equilibrium equations.

You don't have to solve the equilibrium equations in b). The given problems should be answered in terms of the arrival intensities  ς, the average service time 1/Ω, and the equilibrium probabilities P(i,j).
 
c) Give the average number of customers in the queue.
d) Give the average waiting time per customer.
e) How many counters are open on average?
f) Which percentage of time all counters are occupied?
g) What is the fraction of time counter 2 is occupied?
h) Find out the average length of a period during which counter 1 is not occupied.

problem 6: Consider a queueing system with 1 counter, to which groups of customers arrive according to a Poisson proces with intensity λ. The size of a group is 1 with probability p and 2 with probability 1-p. Customers are served one by one. The service time has exponential distribution with mean µ^-1. Service times are mutually independent and independent of the arrival process. The system might contain at most 3 customers. If the system is full upon arrival of a group, or if the system may contain just one additional customer upon arrival of a group of size 2, then all customers in the group are lost and will never return. Let Z(t) record the number of customers at time t.

a) Describe why {Z(t), t ≥ 0}is a Markov proces and give the diagram of transitions and transition rates.
b) Give the equilibrium equations (balance equations) for the stationary probabilities P_n, n = 0,1,2,3.
c) find out these probabilities P_n, n = 0,1,2,3.
The answers to the given problems might be given in terms of the probabilities P_n (except for (h)).
d) Give an expression for the average number of waiting customers.
e) Give the departure rate and the rate at which customers enter the queue.
f) Give an expression for the average waiting time of a customer.
g) What is the fraction of time the counter is busy?
h) What is the average length of an idle period?
i) Find out from (g) and (h) the average length of a period the system is occupied (= at least 1 customer in the system).
j) Determine the rate at which groups of size 2 enter the queue?

problem 7: Consider the open network in the given figure. The queueing system coprises of 4 queues, 1, 2, 3 en 4. Queues 1 and 2 are department I, queues 3 and 4 are department II. The numbers at the arrows provide the transition probabilities for customers routing among the stations, thus a customer which leaves queue 4 routes to queue 3 with probability 2/3, and leaves the network with probability 1/3. Each station has a single server, and each customer arriving to a queue can enter. Service is in order of arrival. Service times have exponential distribution with means 1/µ₁= 1/4, 1/µ₂= 1/3, 1/µ₃ = 1/2, 1/µ₄ = 1. The arrival intensity to station 1 is γ1 (Poisson). [Note: queue i refers to the system comprising of the waiting room plus the server, i = 1,2,3,4.]

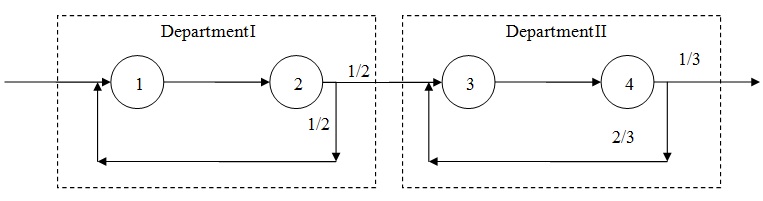
a) Formulate the traffic equations and solve such equations.
b) Provide the stability condition?
c) Give the equilibrium distribution of the queue length at each of the stations 1, 2, 3 and 4.
d) Give the joint distribution of the queue lengths at the stations (product form).
e) Give for each station the average number of customers in the queue, and the average sojourn time of a customer at that queue.
f) Give an expression for the average sojourn time in Department II.

problem 8: Consider the closed network of the given figure. The number at the arrows provide the transition probabilities for a customer leaving the queue to route to a subsequent queue. Every station consists of a single server, and all arriving customers might enter the station.

Service is in order of arrival. The service times have an exponential distribution with with: µ₁= 4, µ₂ = 3, µ₃ = 2, µ₄= 1.

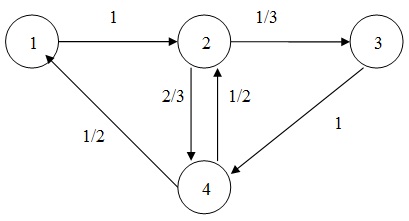
a) Give the joint stationary distribution for the number of customers in the four stations for m = 1, 2, and 3 (m = total number of customers in the network).

b) Obtain by using Mean Value Analyse the average number of customers and the average sojourn time in the four queues for m = 1, 2 and 3.

c) Find out for m = 1 the average time for a customer to return for the first time to station 1.