problem 1: Duality

Recall the max flow problem:

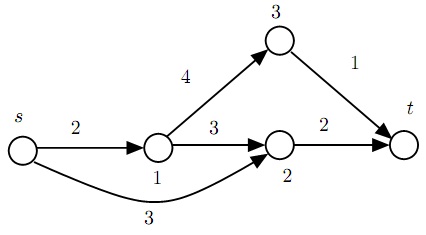
max x_2t + x_3t
x_s1 = x₁₂ + x₁₃
x_s2 + x₁₂ = x_2t
x13 = x3t

0 ≤ x_s1 ≤ 2
0 ≤ x_s2 ≤ 3
0 ≤ x₁₂ ≤ 3
0 ≤ x₁₃ ≤ 4
0 ≤ x_2t ≤ 2
0 ≤ x_3t ≤ 1

A) prepare the dual of the above max-flow problem.

B) Solve both problems with AMPL, and for each print the values of the variables and the values of the dual variables (if a problem has a constraint c1, its dual value can be displayed with the command “display c1.dual;”). Verify that the numbers correspond between primal and dual, and that the optimal solution of the primal and the dual is in accordance with duality.

C) Show the minimum cut that results from solving the dual problems.

D) Consider replacing the objective function in the max cut problem with max x_s1 + x_s2 which gives an equivalent formulation of the max-flow problem. How does the dual formulation change? describe why it is equivalent to the first dual problem.

problem 2: Complementary slackness and duality

Consider the following LP problem:

min x₁ + 3x₂ + x₃ − x₄
s.t. x₁ + x₂ + x₃ + x₄ ≥ 0
x₁ + x₂ − x₃ − x₄ ≥ 1
x₂, x₃ ≥ 0 x₁, x₄ ≤ 0.

A) Unique primal-dual solutions.

• Find a feasible solution (by trying a few guesses) and compute its associated value of the objective function, z_primal.

• prepare the dual.

• Find a feasible solution to the dual (just pick one) and compute its associated value of the objective function, zdual, and check, according to weak duality, that it is not less than zprimal.

• Solve the dual through the graphical method.

• After finding the optimal value of the dual variables, use complementary slackness to find the optimal value of the primal variables.

• Solve both primal and dual problems in AMPL. Print out the solutions.

B) Multiple primal solutions.

• Change the right hand side of the second constraint to -1. How would the dual change?

• Solve the new dual problem graphically.

• Again use complementarity to derive the primal solution. Do you get a unique primal solution or do you get more than one? Can you find all primal optimal solutions? (Hint: all feasible solutions that satisfy complementarity are optimal).

• Solve both primal and dual problems in AMPL. Print out the solutions.

• For the primal problem which of the multiple solutions do you obtain? Can you modify the primal problem a little to obtain a different solution from the optimal set?

problem 3: Linear Programming

Consider the following optimization problem:

min x
s.t. x ≥ max{a₁, a₂, . . . , a_n}

Reprepare this problem as a Linear Programming Problem. What is the solution of this problem? prepare the dual of this problem. From duality theory and complementary slackness give a simple formula for the optimal solution of the dual.