Instructions: Answer each of the given problems. Use Lindo to resolve all problems. Show all work by describeing variables, stating suppositions, illustrating model and showing output solution to the problem. The work must be completed in a word file and should be downloaded by the due date. You should as well upload answers to the excel answer template. It is advisable that you put all work in the excel template by copy and pasting lindo output, using text, and so on.

problem 1: Market Research Real Estate:

A market research firm has been retained to conduct focus group interviews for a real estate company. Plans are made to categorize participants to age: over 45 or 45 and under and as to whether or not they have recently bought and/or sold a house (in the last two years). Specific guidelines have been developed:

• At least 100 people should be selected.
• At least 75 percent of the participants should have bought or sold a house recently.
• Of those who have not bought or sold recently, at least 40 percent must be over 45 years of age.
• No more than 40 percent of participants must be 45 or under.

There are preliminary screenings with associated costs. The cost for each and every participant starts at $10. Additional contact with those over 45 increases the cost by $12. Additional time with the recent buyers and sellers adds $7 to the cost of comprising those participants.  Formulate a linear integer programming model to find out the amount of any kind of participants which minimizes total cost. Use integer programming to establish whole numbers for the solution variables

problem 2: Coffee Beans:

Mrs. Olsen, a coffee processor, markets three blends of coffee. They are; Brand X, Minim and Taster's Reject. Olsen uses two kinds of coffee beans to make the three distinct brands; Columbian and Mexican Beans. The given chart lists the composition of the blends:

Ms. Olsen has already purchased 20,000 pounds of Columbian beans at 90 cents per pound, and she has purchased 30,000 pounds of Mexican beans at 50 cents per pound. At such, these resources are available for use. Unused Columbian beans can be sold at cost to the other processor, though unused Mexican beans can be sold only for 35 cents per pound. Due to warehouse space limitations, Ms. Olsen should dispose of all unused beans.

Brand X sells for $2.60 per pound, Minim sells for $2.50 per pound, and Taster's Reject brings $2.34 per pound. All three products have similar production and packaging costs of $1.20 per pound.

Ms. Olsen is interested in finding out the production schedule which will maximize profit. Formulate a relevant linear programming model or this problem to maximize profit and find out the solution.

problem 3: McDonald and Thomas Advertising Agency:

McDonald and Thomas Advertising Agency has been hired to put altogether an advertising plan for the Healthy Heart Charity Banquet.  The advertising media under consideration are listed in the table shown below:

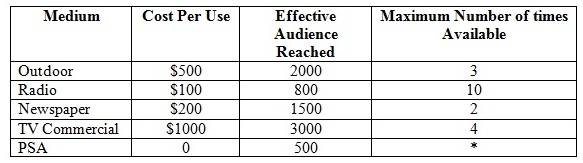
* The TV station will award up to three public service announcements (PSA) for each commercial purchased.

The budget for the campaign is $6000. Every medium should be used at least once. The total number of appearances on TV (comprising PSA) must be no more than twice the number of all the other advertisements. Develop a linear programming model which list objective function and constraints to maximize the efficient audience reached. Use integer programming to make the variables in whole numbers

problem 4: Susan Wong’s Personal Budget

After Susan Wong graduated from State University with a degree in Operations Research, she went to work for a computer systems development firm in the Washington, D.C., area. As a student at State, Susan paid her normal monthly living expenditures for apartment rent, food and entertainment out of a bank account set up by her parents. Each month they would deposit a particular amount of cash into Susan's account. Her parents as well paid her gas, telephone and bank credit card bills, which were sent directly to them. Susan never had to worry regarding things like health, car, homeowner’s, and life insurance; utilities; driver's and car licenses; magazine subscriptions; and so forth. Therefore, while she was used to spending in a particular monthly budget in college, she was unprepared for the irregular monthly liabilities she encountered once she got a job and was on her own.

In some months Susan's bills would be modest and she would spend accordingly, only to be confronted the next month with a big insurance premium, or a bill for property taxes on her condominium, or a large credit card bill, or a bill for a magazine subscription, and so forth the next month. These unexpected expenditures would result in months when she could not balance her checking account; she would have to pay her bills with her bank credit card and then payoff her accumulated debt in installments while incurring high interest charges. By the end of her first year out of school she had hoped to have some money saved to start an investment program, though rather she found herself in debt.

Frustrated by her predicament, Susan decided to get her financial situation in order. First, she sold the condominium that her parents had helped her purchase and moved into a cheaper apartment. This gave her adequate cash to clear her outstanding debts with $3,800 left over to start the New Year with. Susan then decided to use some of the operations research she had learned in college to help her develop a budget. Specifically, she decided to develop a linear programming model to help her decide how much she should put aside each month in short-term investments to meet the demands of irregular monthly liabilities and save some money.

First, Susan went via all of her financial records for the year and find outs her expected monthly liabilities for the coming year, as shown in the given table:

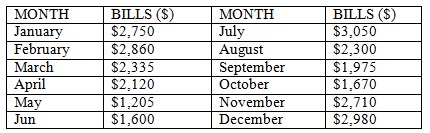
Susan's after-taxes-and-benefits salary is $29,400 per year, which she receives in 12 equivalent monthly paychecks which are deposited directly into her bank account.

Susan has decided that she will invest any money she does not use to meet her liabilities each month in a one-month, three-month, or seven-month short-term investment vehicles, instead of just leaving the money in an interest-bearing checking account. The yield on one-month investments is 6% per year nominal; on three-month investments the yield is 8% per year nominal; and on a seven-month investment the yield is 12% per year nominal. As part of her investment strategy, any time one of the short term investments comes due she employs the principal as part of her budget, though she transfers any interest earned to another long-term investment (which she does not consider in her budgeting process). For illustration, if she has $100 left over in January which she invests for three months, in April when the investment matures she uses the $100 she originally invested in her budget, but any interest on the $100 is invested elsewhere. (Therefore, the interest is not compounded over the course of the year.)

Susan wants to develop a linear programming model which will maximize her investment return during the year so she can take that money and reinvest it at the end of the year in a longer-term investment program. Though, she does not have to confine herself to short-term investments that will all mature by the end of the year; she can continue to put money toward the end of the year in investments that won't mature until the following year. Her budgeting process will continue to the next year, where she can take out any surplus left over after December and reinvest it in a long term program if she wants to.

Develop a linear programming model that to help Susan find out her best investment options to maximum her return. (Hint: You need to create variables which represent monthly investment options. Your objective is maximize return taking into account that money invested each month is left over after expenses have been paid)

problem 5: The Hoggs Corn and Wheat Farm

The Hogg Company is a group of Oklahoma agricultural producers. The Hoggs want to derive a production process which will satisfy their goals. Such farmers can produce corn, wheat, and/or hogs. The acreage they can cultivate for crops is 1100 acres, of which 600 acres is for corn production and 500 acres for wheat production. The Hogs have a maximum of 2000 hour of labor available for crop operations and 600 hour of labor for their hog operation. Corn production needs 1.6 hour of labor per acre, wheat requires 2.0 hour of labor per acre, and the hog operation needs 20 hour of labor per hog unit. This farm can produce 120 bushel of corn per acre and 32 bushel of wheat per acre. Corn and wheat can be sold on the market at $2.50 per bushel and $2.35 per bushel, respectively, and/or can be used as feed in the hog operation. As well, corn and wheat might be purchased from the city feed store at $2.70 per bushel and $2.55 pr bushel, correspondingly, for feeding the hogs. The hog unit needs 169.1 bushel of feed throughout a single production period. The corn and wheat employed as hog feed can be transformed into corn equivalent units; that is, 1.1 bushel of wheat equals 1 bushel of corn.

The cost per acre to produce corn and wheat are $146.40 per acre and $48.60 per acre. The returns to the hog operation are $919.20 per hog unit. A hog unit is a sow and her litter, which are sold on the market. Returns to the hog operation are net values, for illustration, after maintenance and replacement stock cost.

The Hogg Company is considering the given strategy:

Strategy 1:

As the goal with the maximum priority, P1 they would like to see returns to the agriculture operation of at least $100,000. As their second priority, P2, at least three fourths of the land available for corn production and at least one-half of the land available for wheat production must be planted. The producers as well desire that the under-planting of corn be weighed three times greater than that for wheat. The third and last priority goal P3, is that the hog operation be no greater than 40 hog units.

Formulate the problem in a goal programming format and resolve for strategies 1 and 2.  Discuss the outcomes of whether the goals were achieved in each strategy and the corn, wheat and hog production output

problem 6: Shale Oil Co.

Shale Oil, situated on the island of Aruba, has a capacity of 600,000 barrels of crude oil per day. The final products from the refinery comprise two kinds of unleaded gasoline; regular and premium.  The refining procedure encompasses four phases:

a) The pure crude flows via a distillation tower which produces a feedstock.

b) The feedstock output breaks up into two paths; the first path includes feedstock flowing into a cracker unit which refines the mixture into a gasoline stock. The second path has a part of the feedstock flowing into the blender unit.

c) The gasoline stock (from the cracker unit) feeds into the blender.

d) The blender unit produces the final product, regular or premium gasoline. Both the regular and premium gasoline can be generated from either the feedstock or the gasoline stock throughout the blending process, though at different production costs. The company estimates that the net profit per barrel of regular gasoline is $5.20 from feedstock and $7.70 from gasoline stock. The corresponding profit values for the premium are $10.40 from the feedstock and $12.30 from the gasoline stock. According to design specifications, it takes five barrels of crude oil to generate one barrel of feedstock. The cracker units can’t use more than 40,000 barrels of feedstock per day. All remaining feedstock is employed directly in the blender unit to produce the end product gasoline.

The demand limits for regular and premium gasoline are 80,000 and 50,000 barrels per day.

a) Find out the optimum production schedule for the refinery.

b) Assume that the capacity of the distillation tower can be raised to 650,000 barrels per day at an initial cost of $3,500,000 and a daily maintenance cost of $15,000 per day. Could you see a return on the investment within one year of operation? (Suppose annual operating days = 250, answer the problem devoid of rerunning the lindo output, use sensitivity analysis)