1) Consider a Markov chain C1,C2, . . . .

(a) Prove that the joint probability of the first n steps is

p(C1, . . . ,Cn) = p(C1)^π∏_t=2p(C_t| C_t-1).

(b) Hence prove that, for any r < s < t p(C_r, C_s,C_t) = p(C_r) p(C_s|C_r) p(C_t | C_s).

(c) Hence prove that C_r and C_t are conditionally independent given C_s.

2) For an m-state Markov chain C_t with transition matrix G,
(a) prove that the marginal state probabilities at times t and t + 1 are related through

u(t + 1) = u(t) τ,

where u(t) is row vector (p(C_t = 1), . . . , p(C_t = m)).

(b) Hence prove that u(t + k) = u(t) τ^k                          (*)

for any integer k>=0.

(c) Under what conditions would (*) hold for k < 0?

3) For a general discrete homogenous Markov chain with transition matrix G and a specified initial distribution u(1), prepare an R function to do the following:

(a) compute the marginal distribution u(t) from t = 1 up to a specified time t = n

(b) plot the results.

• use operator %*% for matrix multiplication

• use rbind to collect vectors into rows of a matrix U

• use matplot(c(1:n),U,type="l") to plot them in a single plot.

Your R function should contain plenty of comments documenting its inputs, outputs and internal steps.

4) A discrete homogenous Markov chain has transition matrix

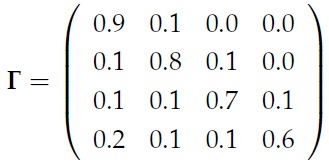
(a) Using your R function from Exercise 4, plot the marginal distribution u(t) for t = 1, . . . , 20, assuming the chain starts in state 1.

(b) Repeat part (a), assuming the chain starts in state 4.

(c) Deduce theoretically the stationary distribution δ of this chain.

(d) Compare your results from parts (a)–(c).

5) A discrete homogenous Markov chain has transition matrix

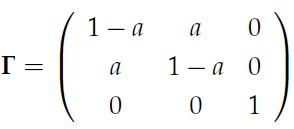
where 0 < a < 1.

(a) Show that  δ= ( 1/3 , 1/3 , 1/3) is a stationary distribution of this Markov chain.

(b) Are there other stationary distributions of this chain?

(c) Comment on your conclusion.

6)a) prepare an R function to generate a sequence of a given length from an m-state homogenous Markov chain with given transition matrix and initial state. As always, your code should contain plenty of comments. Hint: use sample(c(1:m), size=1, prob=p) to sample a single value from distribution p.

(b) Use this function to generate a sequence of length 100 from a Markov chain with initial state 1 and transition matrix

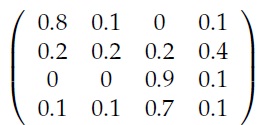
(c) From the resulting sequence, estimate the transition matrix, showing all working.

(d) Compare the true and estimated transition matrices.

7) (a) prepare an R function to estimate the transition matrix of a discrete homogenous Markov chain from a given sequence of observations.

(b) Repeat Exercise E2.7b, this time generating a sequence of length 1000. For each value of k in 100, 200, . . . , 1000, estimate the transition matrix from only the first k observations, using your function from part (a).

(c) Plot these estimated transition matrices against k. Hint: use function matplot.

(d) Comment on your results.

8) N independent sequences, each of length n, are generated from a discrete homogenous Markov chain with transition matrix τ, with initial states drawn from an unknown distribution f .

(a) prepare down the likelihood for such data.

(b) Derive the MLEs of f and τ.

(c) Comment on your results.