problem 1: Suppose that there is a Beta(2,2) prior distribution on the probability θ that a coin will yield a "head" when spun in a speci?ed manner. The coin is independently spun 10 times, and "heads" appears 3 times.

a) find out the posterior mean.
b) find out the posterior variance.
c) find out the posterior probability that .45 ≤ θ ≤ .55.

problem 2:Consider x _˜ Normal(θ,1), θ _˜ (0, 1) and the loss L(θ, δ) = e^-3θΛ2/2(θ - δ)². Derive the estimator that minimizes the posterior expected loss.

problem 3: Suppose X₁, . . . ,X_n has Normal(θ,52) density and a Cauchy(0,1) prior on θ is considered. Suppose sample mean and sample variance are 25 and 49 respectively and sample size is 50. Note that the Cauchy(0,1) density is:

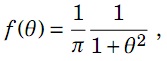
a) Use the Metropolis – Hastings algorithm to sample θ from the posterior distribution. Sample 10,000 θs and take the initial value θ^[0] = 0. Show your R program, trace plot, acf plot, and histogram of the 10,000 θs. Give the estimate of θ², i.e., E[θ²|X₁, . . . ,X_n].

b) Use the fact,

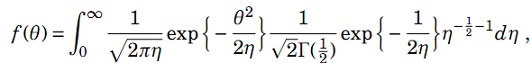
It says, conditional on η,θ has Normal(0, η) distribution and marginally, η has Inverse-Gamma(1/2,1/2) distribution. Derive the posterior distributions of θ|η,X₁, . . . ,X_n and η|θ,X₁, . . . ,X_n. Use Gibbs Sampler algorithms to sample θ and η iteratively from the posterior distributions. Sample 10,000 θs and 10,000 ηs and take the initial values θ^[0] = 0 and η[0] = 1. Show your R program, trace plots, acf plots, and histograms of both 10,000 θs and 10,000 ηs. Give the estimate of θ², i.e., E[θ²|X₁, . . . ,X_n].

problem 4: A bivariate Normal variable x = (x₁, x₂)' has density

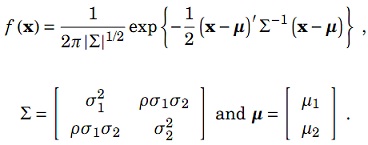
The Random Walk Metropolis – Hastings algorithm is employed to sample random variates from the distribution. A R program is listed below for the purpose.

mu1 <- 1
mu2 <- 0
sigma1 <- 1
sigma2 <- 2
rho <- 0.5
xsamples <- matrix(rep(0,2*10001),10001,2);
xsamples[1,] <- c(0,0);
for (i in 2:10001) {
Y <- xsamples[i-1,1] + rt(1,2);
U <- runif(1,0,1);
condmean <- mu1+rho*sigma1/sigma2*(xsamples[i-1,2]-mu2);
condvar <- sigma1*sigma1*(1-rho*rho);
rho0 <- min(dnorm(Y,condmean,sqrt(condvar))/
dnorm(xsamples[i-1,1],condmean,sqrt(condvar)),1);
if (U<=rho0) {
xsamples[i,1] <- Y;
} else {
xsamples[i,1] <- xsamples[i-1,1];
}
Y <- xsamples[i-1,2] + rt(1,2);
U <- runif(1,0,1);
condmean <- mu2+rho*sigma2/sigma1*(xsamples[i,1]-mu1);
condvar <- sigma2*sigma2*(1-rho*rho);
rho0 <- min(dnorm(Y,condmean,sqrt(condvar))/
dnorm(xsamples[i-1,2],condmean,sqrt(condvar)),1);
if (U<=rho0) {
xsamples[i,2] <- Y;
} else {
xsamples[i,2] <- xsamples[i-1,2];
}
}

a) Identify the parameter values for the mean and the covariance matrix of the bivariate Normal distribution according to the program.
b) State the conditional distribution of x₁ given x₂.
c) Briefly describe the program.