TASK A: Minitab analyses for Case Study
The data is listed in the table below and may be copied into Minitab (best to use the file task3.mtw). Use the menu item Stat_DOE_Factorial_Custom design to indicate that Minitab should use the information in the worksheet to set up a 2-level factorial design object. (The results will be seen in the Project Manager.)You should indicate that the worksheet data are coded but also enter the real “uncoded” values in the Low/High table.
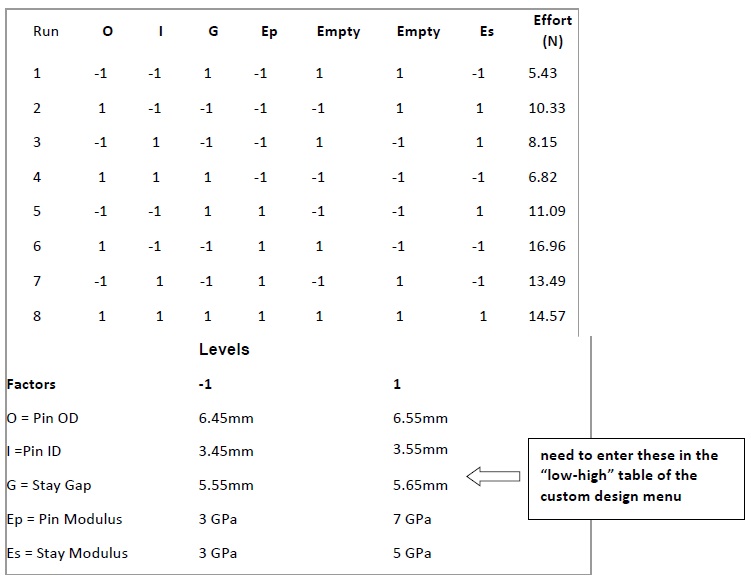
problem1) Use the Factorial/Factorial Plots option to display main effects plots for the response variable (Effort) using both coded and uncoded representations of the design variables (factors) including the “empty” columns. State what the plots suggest about important sources of variation in effort.
problem2) Now apply the Analyze Factorial Design item to the response variable effort choosing: (i) terms up to order 1 leaving out the empty columns, (ii) results with no alias table, (iii) graphs with normal plots of the main effects with alpha set at 0.1.
(a) Display the tabular form of the fitted equation with factors in coded form and use the 1 need to enter these in the equation to predict the mean effort for a flap having Pin OD = 6.45, Pin ID = 3.50, Stay Gap = 5.65, Ep = 5 and Es = 4. [Hint: factors which are exactly on target are coded as zero. You can just plug the values into the coded form of the fitted regression model, making sure to use coefficients not effects.]
(b) Display the normal plot and point out important similarities and differences between it and the main effects plots from problem 1. What conclusion does it suggest about important factors to consider?
(c) Add the empty columns back into the terms to be fitted, run the analysis menu again and display the resulting normal plots of the main effects. describe how this display further supports the conclusions you drew in part (b) about unimportant factors.
problem3)
(a) Try simply regressing the column Effort on the 5 design variables with the variables in coded form , leaving out “empty’ columns. (Use the Stat_Regression_Regression menu.) How do the results compare with part 2?
(b) Repeat the regression but now replace O and G by the interference (i.e. a column containing the difference O – G) and leave out I and Es and any empty columns. Interpret the result. You can still use the coded form of the design variables.
problem4) Now use Create Factorial Design to create an 8 run expt with 7 factors. (It should open a new worksheet within your Minitab project) Use the default settings, but under Options do not randomize order, and choose summary and alias tables under Results. Display the design and compare it with that used in the lecture notes. Is it essentially the same design?
Optional: Use column multiplication to check the aliasing of C and DG. Referring back to the design used for the filler flap robustness investigation, could this aliasing create any doubt about the conclusions we have drawn about important design factors?
TASK B: Design optimisation
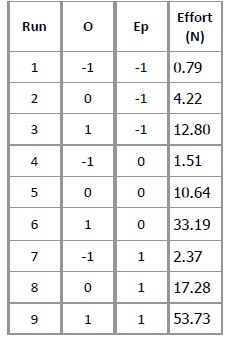
Enter the data from the above table in Minitab. Carry out the following tasks:
problem1) Fit and plot a quadratic response surface (with both surface plot and contour plot) relating the pin diameter and modulus to the effort. (Use DOE/Response Surface design.)
problem2) Find a target value for pin diameter that achieves the target effort (10.5N) established by the researchers (task 1 of the case study), when the pin modulus is at its mid-value used in this experiment.
problem3) Determine whether the expected variation in pin modulus can be accommodated within the acceptable range of efforts established in task 1 (of the case study). Assume that typical manufacturing variation in pin diameter is ±0.05mm and that variation in the pin modulus is the variation find outd as “ x¯ ± 3s ” Comment on any assumptions you are making
problem4) In the light of your conclusions from part 3, how might you go about ensuring that the general flap design is comfortably able to achieve its objective regarding effort?