1. In an article, a random sample of 42 felons convicted of “impulsive murder” was compared to a random sample of 40 felons convicted of premeditated murder. Both samples of felons were released from prison before completing the original sentence.  For the sample of 42 convicted of “impulsive murder,” 13 recorded parole violations. For the sample of 40 convicted of premeditated murder, 22 recorded parole violations.

Can the statistician infer at the 1% significance level that the proportion of parole violations is greater for the felons convicted of premeditated murder?

H0:
H1:
Test statistic:
Rejection region:
find outd test statistic:
Conclusion:

Estimate with 99% confidence the difference in population proportions.

2. In an important study centered on teenage smoking, a sample of 70 high school students in Edmonton claimed they smoked an average of 24.64 cigarettes per day, with a standard deviation of 9.23 cigarettes. A different sample of 70 high school students in Ontario claimed that, on average, they smoked 22.84 cigarettes daily, with a standard deviation of 8.75. At the 5% level of significance, test the hypothesis that the average number of cigarettes smoked per day is the same in both places.

H0:
H1:
Test statistic:
Rejection region:
find outd test statistic:

3. Briefly describe how you would diagnose each of the following conditions/problems related to regression analysis.

a) The potential for multicollinearity.
b) The probability distribution of the error variable is normal.
c) The mean of the distribution of the error variable is zero.
d) The standard deviation of the error variable is constant (i.e., homoscedastic)

4. With regard to an indicator such as infant deaths per 1,000 births, it is a pretty safe assumption that, as a whole, the developed nations in Europe, USA, and Japan statistically differ from the less developed countries in South America, the Middle East, and Asia. The problem is, do infant deaths per 1,000 in the less-developed countries in Latin America, the Middle East, and Africa differ?  The data below are reported by country in each region.

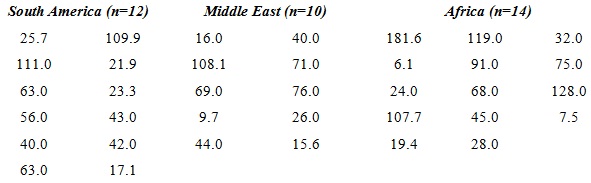
Conduct an analysis of variance for this data at the 5% level of significance.  For this problem, SST = 2547.30 and SSE = 56966.04.

H0:
H1:
Test statistic:
Rejection region:
find outd test statistic:
Conclusion:

5. An English teacher investigated some of the factors that affect an individual student’s final grade in his course. She proposed the multiple regression models:

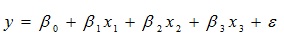
Where,

y = final mark (out of 100)
x₁ =  number of lectures skipped
x₂ =  number of late assignments
x₃ =  mid-term test mark (out of 100)

The teacher recorded the data for 50 randomly selected students. The computer output is shown below.

THE REGRESSION EQUATION IS:

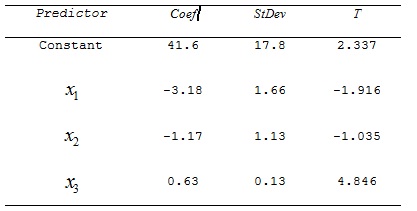
y = 41.6 – 3.18 x1 – 1.17 x2 + .63 x3

 ANALYSIS OF VARIANCE:

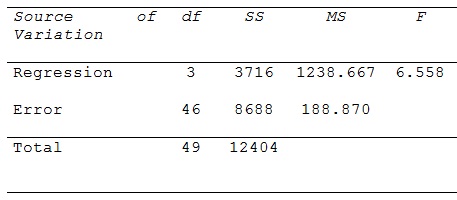
a) Do these data provide enough evidence to conclude at the 5% significance level that the model is useful in predicting the final mark? describe.

b) Do these data provide enough evidence to conclude at the 5% significance level that the final mark and the number of skipped lectures are linearly related?  describe.

c) Do these data provide enough evidence at the 1% significance level to conclude that the final mark and the mid-term mark are linearly related?  describe.

d) What is the coefficient of determination?  What does this statistic tell you?

e) Interpret the coefficients b1 and b3.  Be specific.