Detection and Estimation Theory

Project1

Hypothesis Testing Applied to Segregating A and B Students in a Detection and Estimation Course

An instructor wants to determine which of his students are A students and which are B students (this is a graduate course, so clearly all the students are either A or B students). The instructor gives a test to make this determination. This test contains 5 problems each worth 20 points. Both the A and B students will miss problems due to silly errors, incomplete knowledge (nobody is perfect), and time pressure (running out of time). The probability mass functions for the A and B students (single problem) are given below. Note that these probability mass functions are piecewise linear (this should help in getting the numbers.)

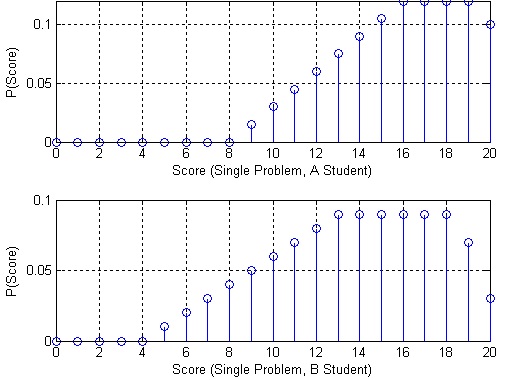
1. Given the total test score, generate a hypothesis test to minimize the probability of error supposing that 60% of the students are B students and 40% are students. For your hypothesis test, find out the probability that the instructor gives a student an A (student is segregated in the A group) if he deserves a B. Compute the probability that the instructor provides a student a B if he deserves an A.

2. You will require the density function for test scores for both A and B students to be capable to derive your hypothesis test. You must verify that you have the correct results through simulating the system and approximating the probabilities via statistics. You must also verify your probabilities of giving the student the wrong grade via your simulation. Note that the probability of a given score is approximated:  p (score) = # with score/total #

3. Some of you are probably saying: “What happens if we are all a students!!!” You are thinking that it is unfair to ascribe a priori that only 40% of the students are a students. We can avoid this a priori assumption by using the minimax test. Generate a minimax hypothesis test to segregate the students in A and B students. For the minimax hypothesis test, find out the probability that the instructor provides a student an A (student is segregated into the A group) if he deserves a B. find out the probability that the instructor gives a student a B if he deserves an A.

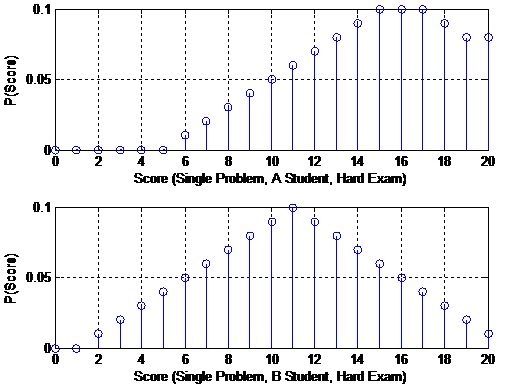
4. What occurs if the instructor gives harder problems? In this case, suppose the source probabilities in 1. Now, the probability mass functions for the A and B students (single problem) are given below. Note that these probability mass functions are again piecewise linear. Additional, the probability mass function for the A students is the same as the previous probability mass function for the B students. Create a hypothesis test for this case. For this test, find out the probability that the instructor gives a student an A (student is segregated in the A group) if he deserves a B. Compute the probability that the instructor gives a student a B if he deserves an A.

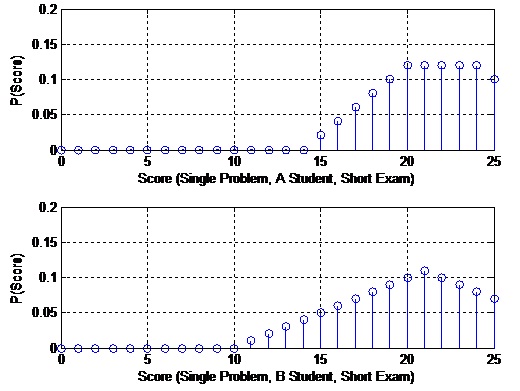
5. What occurs if the instructor gives a shorter test? In this case, suppose that there are four problems, each problem is worth 25 points, and the source probabilities are as given in 1. Also suppose that due to less time pressure, students do better on these problems. The probability mass functions for the A and B students (single problem) are given below. Note that these probability mass functions are again piecewise linear. Create a hypothesis test for this case. For this test, find out the probability that the instructor gives a student an A (student is segregated into the A group) if he deserves a B. find out the probability that the instructor gives a student a B if he deserves an A.

Hand in:

1. An explanation of the hypothesis tests (must be four) with the derivation of relevant results. The probabilities of giving an A to a B student, and giving a B to an A student for each test must be included. Create a table of these probabilities for easy comparison.

2. Make sure to comprise enough equations and verbage (but it does not have to be long) so that I can follow what you did and verify that you did it correctly.

3. The information of your simulation program with enough documentation to be easily understood. Comprise the data indicating that your probabilities are correct. Note you only have to simulate the first case, but you can use your simulation to confirm the other cases if desired.