problem 1: The probability density function (pdf) of X is given by:

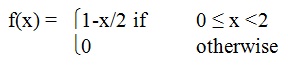
a) Verify that that f(x) is a legitimate pdf.                 

b) Sketch the graph of the pdf function.              

c) Find the distribution function of X and sketch the graph.

d) Compute P(1< X < 2.3).                       

e) Find the expected value and the variance of X.      
   
problem 2: Let the distribution function of X given by:

         ¦    0                                    if    x< -2
F(x) =      1/2 + (3/32)(4x -x³/3)        if    -2 ≤ x < 2
         ¦    1                                    if    x ≥2

a) Graph the distribution function.

b) Compute P(X< 1).                

c) Compute P(0.5< X <2.4). 

d) Find the median.                    

e) Find the density function of X.