Carry out the following operations.

a) Find out sample correlation coefficients of (I) age with dry weight, and (2) age with log 10 dry weight. Interpret your results.

b) For each straight-line regression, find out r2 directly by squaring r obtained in part (a); also determine r2 from computer output or from formula r2 (SSY - SSE)/SSY. Interpret your results.

c) Based on preceding results. Which of the two regression lines gives the better fit? Describe. Does this agree with your earlier conclusion?

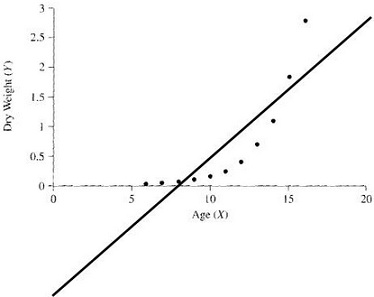
We get the following for Y versus X

Now, for Z versus X we get

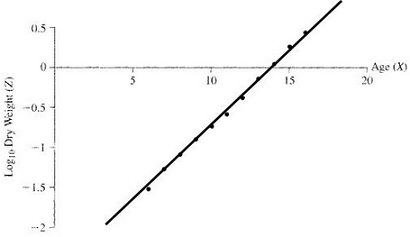
It is clear that second regression has much better linear fit. Actually, in the Y-versus-X model, 74.42% of variation is explained, whereas in the Z-versus-X model, 99.83% of variation is described.