problem 1:

a) prepare a brief note on spatial and temporal data.

b) Compute standard deviation and variance for the given data. The table shows the number of students falling in various classes according to the marks obtained in the Geography paper.

problem 2:

a) prepare a note on the skewness and kurtosis.

b) In an area of stony waste the mean size of the class was 16 mm with standard deviation of 2 mm. If the sample of class is chosen at random, find out the probability that it will have a size:

• Between 10 mm and 21 mm
• More than 18 mm
• Exactly 10 mm
• At least 17 mm

problem 3:

a) describe the Binomial Probability of the Distribution.

b) The given table gives decadal population of India. By using least square method, obtain best fit equation. Estimate the population of India for 2011.

(Population in millions)

problem 4:

a) prepare properties of time series.

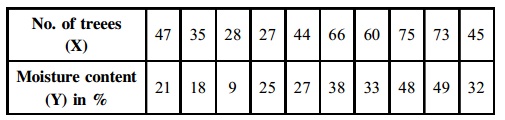
b) The table gives data of number of trees (X) and moisture contain in the soil (Y) of a species in randomly chosen quadrants. Determine the Pearson’s product moment correlation coefficient. Test the level of importance at 0.05 and interpret the value.

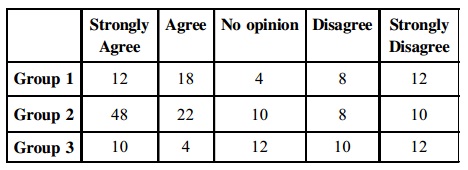
problem 5: A sample survey of 200 university students was taken out to know their opinion regarding the student representative on University Management Council. Apply the Chi square test to test the hypothesis at 0.05 level of importance to know whether there is important difference in opinion among the three groups.

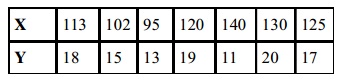
problem 6: The given data represents rainfall in cm (X) and yield of paddy in quintals (Y) per hectare in a district. Find out regression equation for the data. Compute describeed variance and residuals from regression equation and comment on it.

problem 7: prepare brief notes on any two:

a) Concept of residuals and describeed variance.
b) Unbiased random sample.
c) Grouped and ungrouped data.