problem 1: Consider two perfectly negatively correlated risky securities A and B. A has an expected rate of return of 12% and a standard deviation of 17%. B has an expected rate of return of 9% and a standard deviation of 14%. The weights of A and B in the global minimum variance portfolio are _____ and _____, respectively.
 
problem 2: find out the duration of a par value bond with a coupon rate of 8% and a remaining time to maturity of 5 years.
 
problem 3: On September 26, the spot price of gold was $320 per ounce and the price of a December future on gold (three months to maturity) is $322. What would be the price of a March futures contract? The six-month interest rate is 6% per year and the three month interest rate is 5% per year.
 
problem 4: In December 1979 it was possible to buy a January 1980 contract in gold at the New York Commodity Exchange for $487.50 per ounce and sell an October 1981 contract for $614.80 on the same day. Under what condition would this have been profitable? Exactly what could you have done to make arbitrage profit if you had taken these possible? What type of interest rate is relevant in this context?
 
problem 5: Assume that the risk free interest rate is 9% per annum with continuous compounding and that the dividend yield on a stock index is 4% per annum. The index is standing at 78 and the futures price for a contract deliverable in four months is 80. What arbitrage opportunities does this create?
 
problem 6: Regression analysis is one technique often used in studying hedging problems. Using daily data for the previous year, a regression of KOSPI200 cash index returns on near KOSPI 200 futures returns yields the following output:

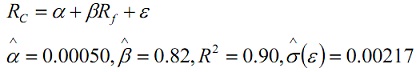
Suppose that you wish to hedge 1-day risk of a $17M KOSPI200 index stock basket. If the current KOSPI200 cash index equals 265, how many near KOSPI200 futures contracts should be sold to minimize risk?
 
problem 7: Suppose that the yield curve is flat at 5% per annum with continuous compounding. A swap with a notional principal of $100 million in which 6% is received and six-month LIBOR is paid will last another 15 months. Payments are exchanged every six months. The six-month LIBOR rate at the last reset date (three months ago) was 7%. What is the value of the swap in terms of both bonds and FRAs?