A random process  is said to be mean square continuous at some point in time , if

(a) Prove that is mean square continuous at time t  if its correlation function,  is continuous at the point 

b) Prove that if  is mean square continuous at time t , then the mean function must be continuous at time t.

(c) Prove that for a WSS process  is continuous at 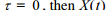 is mean square continuous at all points in time.