MICROECONOMIC ANALYSIS:

Section A:

problem 1: What do you mean by a social welfare function? If you suppose that such a function exists, what properties of social optima would be considered by you? Discuss these properties.

problem 2: Assume that there is a pure exchange economy with 2 consumers and 2 goods. The endowments are w¹ = (2, 4), w² = (4, 3). Consumers are or else identical and they have utility function U(x, y) = x^1/3y^1/3.

a) Make an Edge worth Box for this economy.

b) Give a definition of Pareto Optimal Allocation in this economy. Find out all Pareto optimal allocations and graph them in the Edge worth Box.

c) How would you define a competitive equilibrium for this economy? Solve for the equilibrium and check whether the competitive equilibrium is Pareto Optimal.

problem 3: Two players first simultaneously declare Yes or No. If any of the players declares No, then each player gets 80. If both players declare yes, then they play the given game:

Find out all the subgame-perfect equilibria of the whole game including pure strategies only.

problem 4: What is the theory of Second Best? Prove the theorem by using a diagram.

problem 5: Let the optimal incentive plan be given as:

s (x) = wx+ k where
s(x)= incentive scheme
x = output, w = wage and k = constant 4

A worker can produce x units of output at a cost of C (x) = x²/2 and he can achieve a utility level of u = 0 working elsewhere. What is the optimal wage-labor incentive scheme s(x)₁ for this worker?

Section B:

problem 6: Suppose Kareena’s utility function is u = (y/1000)^1/2. Her initial income when healthy is 36,000. Though, there is a 50% chance that she will face financial loss on being taken ill and the income is likely to decrease by 20,000.

a) Find out the expected value of her income.
b) What expected utility she will have given the possible state of her health?
c) What is the risk premium she will be willing to pay to cover the risk of sickness?

problem 7: Consider the given game given in extensive form:

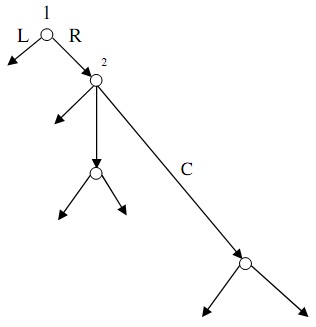
a) Use backwards induction to find out equilibrium of the game.
b) prepare this game in the normal form.