problem 1: In a year, weather can inflict storm damage to a home. From year to year the damage is random. Let Y be the dollar value of damage in a given year. Assume that 95% of the year’s Y = $1,000, and 5% of the years, Y = $15,000.

a) find out the mean and standard deviation of the damage in any year.

b) Consider an ‘insurance pool’ of 100 sufficiently dispersed homes, which implies the damage to different homes can be viewed as independently distributed as random variables. If ? is the average damage to such 100 homes in a year, (i) Find out the expected value of the average damage? (ii) What is the probability that ? exceeds $2000?

problem 2: As problems related to every day Economics involve more than one variable, let us work with two random variables.

Assume that the given table gives the joint PDF (probability distribution function, not Adobe document!!) of two discrete variables, x and Y.

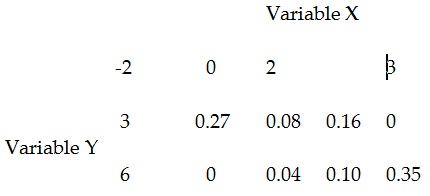
Interpretation of the Table: If the variable X takes on a value, (-2) and the variable Y takes on a value 3, their joint probability is 0.27. In another words, the probability of X = -2 and Y = 3 simultaneously is 0.27. Continuing this, the probability of X = 0 and Y = 3 is 0.08 and so forth.

By using the information given in the table above, compute:

a) Marginal Probability Density Functions of X and Marginal Probability Density Functions of Y.

b) Conditional probability of (X = -2 | Y = 3) and the conditional probability of (X = 2 | Y = 6).

c) Find out the expected value of X, E(X), and expected value of Y, E(Y).

d) Find out the Covariance between X and Y, cov(X, Y).

e) Compute the coefficient of correlation, r.