Red Brand Canners

On Monday, September 13, 1965, Mr. Michael Gordon, Vice President of the operations, asked Controller William Cooper, the Sales Manager Charles Myers, and Dan Tucker the Production Manager to meet with him to discuss the amount of a tomato product to pack that season.  The tomato crop, which had been purchased at planting, was starting to arrive at the cannery, and packing operations would have to be started by following Monday.  Red Brand Canners (RBC) was a medium-size company that canned and distributed a variety of fruit and vegetable products under private brands in the western states.

Cooper and Myers were the first to arrive in Mr. Gordon’s office. The production manager came in some minutes later and said that he had picked up produce inspection’s newest estimate of the quality of incoming tomatoes. According to their report, about 20% of the crop was grade ‘A’ quality and the remaining portion of the 1.5 million pound crop was grade ‘B’.

Gordon asked Myers about the demand for tomato products for the coming year.  Myers replied that they could sell all of the whole canned tomatoes they could produce.  The anticipated demand for tomato juice and tomato paste, on the other hand, was limited.  The sales manager then passed around the newest demand forecasts, that is shown in
Exhibit1. He reminded the group that the selling price has been set in light of the long-term marketing strategy of the company, and potential sales have been forecasted at these prices.

Bill Cooper, after looking at Myers’ estimates of demand said that it looked like the company “should do quite well on the tomato crop this year.” With the new accounting system that had been set up, he has been capable to find out the contribution for each products and according to his analysis the incremental profit on the total tomatoes was greater than for any other tomato products. Thus, he suggested using the whole crop to produce whole tomatoes. In May, after RBC had signed contracts agreeing to purchase the grower’s production at an average delivered price of $0.18 per pound, Cooper had evaluated the tomato products’ contributions (see Exhibit 2).

Dan Tucker brought to Cooper’s attention that though there was ample production capability, it was not possible to produce all whole tomatoes since too small portion of the tomato crop was ‘A’ quality. RBC used a numerical scaling to record the quality of both raw produce and prepared products. This scale ran from 0 to 10, with the higher number representing best quality. Rating tomatoes according to this scale, grade ‘A’ tomatoes averaged nine points per pound and grade B tomatoes averaged five points per pound. Tucker noted that the minimum average input quality for canned whole tomatoes was 8 and for juice it was six points per pound. Paste could be made entirely from grade ‘B’ tomatoes. This meant that whole tomato production was limited to 400,000 pounds.


Gordon stated that this was not an actual limitation. He had been recently solicited to purchase 80,000 pounds of grade ‘A’ tomatoes at$0.085 per pound and at that time he turned down the offer. He felt, however, that the tomatoes were still available.

Myers, who had been doing some computation, said that though he agreed that the company “must do quite well this year” it would not be by canning whole tomatoes. It seemed to him that the tomato cost must be allocated based on quantity and quality, rather than by quantity only as Cooper had done. Thus, he re-evaluated the marginal profit on this basis (Exhibit 3). From his result, RBC must use 1,000,000 pounds of the grade ‘B’ tomatoes for paste, and the remaining 200,000 pounds of grade ‘B’ along with all of the 300,000 pounds of grade ‘A’ tomatoes for juice.

Assignments

Answer the following problems:

problem1. Why does Tucker state that the complete tomato production is limited to 400,000 pounds? (That is, where does the number 400,000 come from?)    

problem2. What is wrong with Cooper’s suggestion to use the complete crop for complete tomatoes?

problem3. How does Myers reach the conclusion that the company should use 1,000,000 pounds of grade ‘B’ tomatoes for paste and the rest of the grade ‘B’ and grade ‘A” tomatoes to produce juice? What is wrong with Myers reasoning?

problem4. What values will you use for marginal profit of each product? Elucidate your rationale.

Set up a linear programming model and solve it with Solver. Suppose it is okay to produce partial cases of each product. Answer sensitivity analysis problems:

problem5. Without including the possibility of the additional purchases suggested by Gordon, formulate as an LP the problem of determining the optimal canning policy. Use the appropriate parameters from one of the exhibits shown below.

problem6. Answer the subsequent problems about the optimal solution:

a. How much of each tomato grade will be used for the production of each product?

b. How much of each product is produced?

c. What is actual average quality per pound of the whole tomato and the juice?

d. What is net profit obtained after netting out the cost of the crop?

problem7. Answer the subsequent sensitivity analysis problems (Answer each problem separately. Consider creating a separate Excel tab for each problem.):

a. Should additional buy of up to 80,000 pounds of grade ‘A’ be undertaken at a price of $0.085? Can you tell exactly how much should be purchased? If more were available, how much should be purchased?

b. Assume the Market Research Department feels that it can increase demand for the juice product by 25,000 cases by starting an advertising campaign. How much should RBC be willing to pay for such a campaign?

c. Assume the price of juice increased 30 cents per case. What will happen to the optimal solution?

d. Assume an additional lot of 50,000 pounds of grade ‘B’ tomatoes becomes available. How much should RBC be willing to pay for this lot?

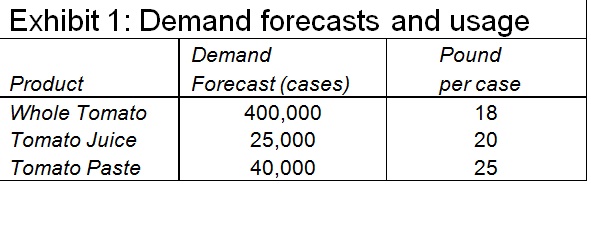
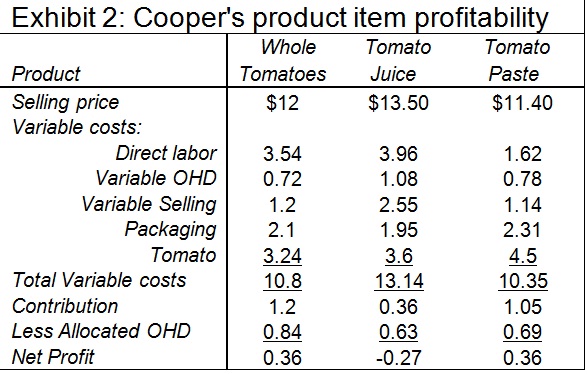
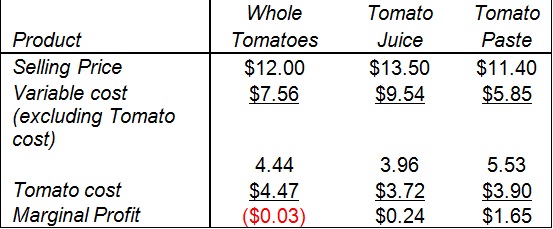
Exhibit 3: Myers' Marginal Analysis   
Calculating the actual cost of grade 'A' and grade 'B' tomatoes:
Z = Cost per pound of 'A' tomato in cents       
Y = Cost per pound of 'B' tomato in cents       
(1) 300,000Z+1,200,000Y = (1,500,000) (18cent)       
(2)  Z/9 = Y/5
           
     Z = 27.96 cents               
     Y = 15.54 cents