problem 1:

i) Why is it essential to model interest stochastically? How would you like to develop a model of the stochastic interest?

ii) Rs.100 deposited 20 years ago has grown at interest to Rs.235. The interest was compounded twice a year. Determine the nominal and effective interest rates?

problem 2:

i) Discuss the difference between classical and Bayesian analysis credibility theories.

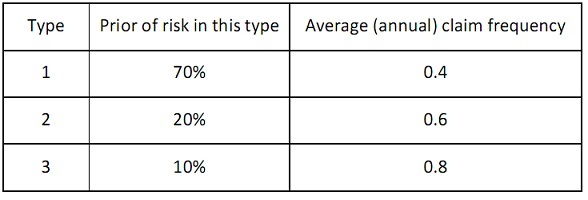
ii) From the given table, a risk is picked at random and we don’t know what kind it is. For this randomly chosen risk, during one year there are 3 claims. Use Bayesian analysis to predict the future claim frequency of this same risk. (Suppose that the kinds are homogeneous).

problem 3: Discuss the methods you would like to use for reinsurance. Justify your choice.

problem 4: Formulate the Lundberg Risk Model. What modifications you might like to introduce in it for providing an alternative?

problem 5: What is a DFA model? Outline its significant components and spell out their significance.

problem 6: describe the main claim reserving models. Given a choice which of such would you like to prefer? Provide reason in support of your answer.

problem 7: Answer the given as directed:

a) prepare a short note on the Survival Function.

b) Distinguish between insurance price setting and finance market pricing.

c) Show that the Black-Scholes formula for the price of a call option gives a price, which tends to max [S – X, 0] as t → T.

d) How would you utilize the binomial tree approach to value an American option on a   stock index whenever the dividend yield on index is a function of time?