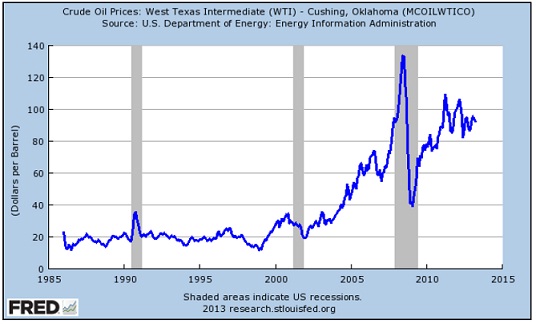
Problem1) Oil Markets Displayed below is the price of one barrel of (WTI) oil over the past few decades. A barrel of oil can be thought of as an asset because it is storable.

For the sake of simplicity, suppose that this is the only asset via which the infinitely-lived representative consumer can accumulate wealth.

Denote by wti_t-1 the quantity of barrels owned by the consumer at the start of period t; denote by S^wti_t the nominal price during period t of one barrel of oil; as usual, let 0 < β < 1 stand for the consumer’s one-period-ahead discount factor, P_t stands for the period-t nominal price of consumption, and Y_t stands for period-t nominal income. Finally, the period-t utility function of the consumer is

u(c_t, d.wti_t)

in which 0t-1 (you can think of this as heat for the oven or for the house, etc.)
Thus, the consumer’s lifetime utility function starting from the beginning of period zero is

^∞∑_t=0βu(c_t, d.wti_t)

a. Using the notation above, construct the period-t budget constraint of the consumer, and provide a ONE-SENTENCE economic comparison of this budget constraint to that in our study of stock-market pricing..

b. Based on your budget constraint in part a above and the lifetime utility function, construct the Lagrangian for the consumer’s optimization AND compute the FOCs for c_t c_t+1, and wti_t.

c. Based on the FOCs you obtained in part b above, compute the period-t oil price. That is, construct the expression

                                                 S^wti_t
(the “…” that appears on the right-hand-side is for you to construct).

d. You can see in the graph displayed above that oil prices have overall been much higher over the past decade than before. Provide a brief explanation that is just based on how the d term in the utility function may have changed over the years. Your explanation should be stated in both mathematical terms AND in economic terms (that is, the economic explanation should not simply be a verbal restatement of the mathematics).