problem 1: Consider the given two probability distributions for sales:

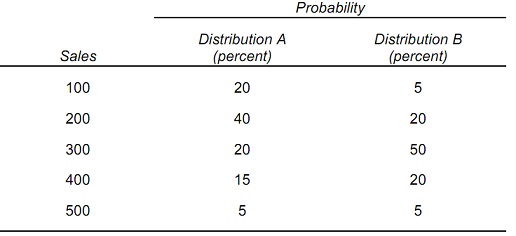
a) Compute the expected sales for both of these probability distributions.

E(Sales_A) = __________
E(Sales_B) = __________

b) Compute the variance and standard deviation for both of the probability distributions.

σ_A² = __________   and σ A = __________
σ_B² = __________   and σ B  = __________

Distribution _____ is more risky than distribution _______.

c) Compute the coefficient of variation for both distributions:

v_A = __________

v_B  = __________

Distribution _____ has greater risk relative to its mean than distribution _____.

problem 2: Texas Petroleum Company is a producer of crude oil which is considering two drilling projects with the given profit outcomes and associated probabilities:

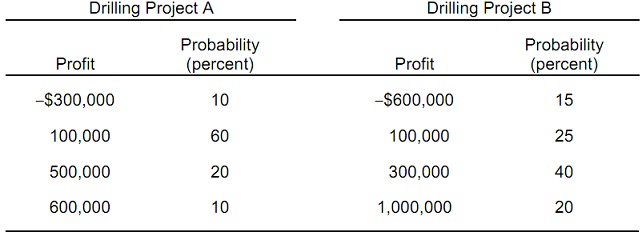
a) Evaluate the expected profit for both drilling projects.

E(Profit_A) = __________   and   E(Profit_B) = __________

b) Based on the expected value rule, Texas Petroleum should choose drilling project _______.

c) find out the standard deviations of both projects:

σ _A = __________   and σ _B = __________

d) Which drilling project has the greater (absolute) risk?

e) Use mean-variance rules, if possible, to decide which drilling project to undertake. Describe.

f) find out the coefficient of variation for both projects:

v_A = __________   and v_B = __________

By using the coefficient of variation rule, Texas Petroleum should choose project _____.

problem 3: A manager’s utility function for profit is  U(π ) = 35π, where  π  is the dollar amount of profit. The manager is considering a risky decision with the four possible profit outcomes shown below. The manager makes the given subjective assessments regarding the probability of each and every profit outcome:

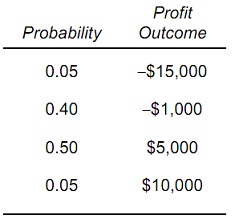
a) The expected profit is _______________.
b) The expected utility of profit is _____________.
c) The marginal utility of an extra dollar of profit is ________.
d) The manager is risk ___________ as the marginal utility of profit is ____________.
 
problem 4: Assume that the manager of a firm has a utility function for profit U(π ) = 12ln(π ), where π is the dollar amount of profit. The manager is considering a risky project with the following profit payoffs and probabilities:

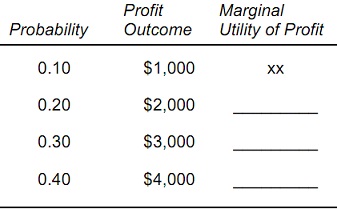
a) The expected profit is _______________.
b) The expected utility of profit is _____________.
c) Fill in the blanks in the following table showing the marginal utility of an additional $1,000 of profit.
d) The manager is risk _________ because the marginal utility of profit is __________.

problem 5: A firm is making production plans for next quarter, but the manager doesn't know what the price of the product will be next month. She believes there is a 30 % chance that price will be $500 and a 70 percent chance that price will be $750. The four possible profit outcomes are:

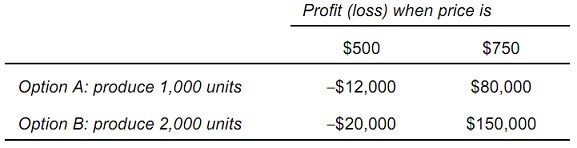
a) Option ______ maximizes expected profit.

b) Option ______ is the riskier of the two options.

c) The manager _____________ (can, cannot) apply mean-variance rules in this decision. If the manager can use mean-variance rules, the manager would choose Option ______.

d) Using the coefficient of variation rule, the manager chooses Option _____.

problem 6: Suppose the manager in Problem 5 has absolutely no idea about the probabilities of the two prices occurring. Which option would the manager choose under each of the following rules?

a) Maximax rule                     _________________
b) Maximin rule                      _________________
c) Minimax regret rule            _________________
d) Equal probability rule         _________________