problem 1: In this exercise we will examine whether a teacher’s physical attractiveness has any impact on student course evaluations. The dataset to use is called teachingratings, and a description of the variables is available as well. You can access these through the course website. Use an α = .05 for hypothesis testing.
We’ll first examine whether our control variables seem to have any predictive power for ratings.
A) We’ll start with some basic dummy variable regressions to test for differences between groups:
a) Regress course_eval on minority. Report the coefficients and p-values. Do minority instructors have significantly different course evaluations compared to non-minorities?
b) Regress course_eval on female. Report the coefficients and p-values. Do females have significantly different course evaluations from males?
c) Run a final regression to test whether the effect of being a minority changes depending on whether the person is female. Report the coefficients and p-values. Can you reject the hypothesis of no effect?
B) Now regress course_eval on beauty, age, age^2 [you’ll need to create this], nnenglish, female, minority, onecredit. Are any variables not statistically significant? Which? This is Model 1. Use Model 1 to answer the following:
a) find out an F-test for the hypothesis that age and age^2 jointly have no effect on course_eval. You can execute this test however you prefer.
b) find out an F-test that female and minority have an equal impact on course_eval. You can execute this test however you prefer.
C) Modify Model 1 so that you can determine whether beauty has a different effect for women than for men. This is Model 2. Report the coefficient and p-value for the interaction variable. Can you reject the hypothesis of no effect of the interaction? Use Model 2 to answer the following:
a) Professor Smith is a man. He isn’t very handsome. He undergoes plastic surgery, which raises his beauty from one standard deviation below the mean to one standard deviation above. What is the predicted change in his course evaluations? [Note: you will have to figure out how to find out a standard deviation in STATA. It isn’t hard. Also, note that the average beauty level in the data has been scaled to equal zero.]
b) Repeat part 1) for Professor Jones, who is a woman.
D) Go back to Model 1. Add two variables to Model 1 that will allow you to determine whether age has a different effect for women than for men on course evaluations. [Note: since age appears twice in Model 1, you will need to create the interaction for both age and age^2.] This is Model 3. Report the coefficients and p-values for the interaction terms. Can you reject the hypothesis of no effect of the interactions?
Use Model 3 results to answer the following:
a) Professor Thomas, a man, begins his teaching career at age 32. Assuming his beauty measure (and all other variables) is unchanged over his career, what is the predicted change in his course_eval score when he retires at age 65?
b) Repeat 1) for Professor Gomez, who is a woman.
problem 2: Estimating Cost and Production Functions
A) Download and input the data.
I have recently downloaded the NBER-CES manufacturing industry database and posted it to ANGEL. I have opted to do this in Excel format. Before you put it into STATA, you should delete all of the data except the stuff you need. What do you need? The rows you need are the ones corresponding to the industry SIC code that has been randomly assigned to you. There is a spreadsheet titled (random SIC codes) which will have your industry. [If curious, you can use Google to determine precisely which industry your SIC code is for. (2011, for ex, is Meat Packing Plants.)]
Additionally, the five variable columns needed for this assignment are
vadd= value added (i.e. output)
pay= total payroll
invest=total capital expenditure
energy=total energy expenditure
year= year of observation
To enter the data into STATA: Copy the data from Excel, including the variable names. In STATA, click on Window-> Data editor. Go to the upper left-hand cell, right click and paste. Tell STATA to use the first line as variable names.
B) Estimate the cost functions:
The total cost function models the total cost of production as a function of output. We need first a measure of total cost, which we will take as the sum of labor, capital and and energy costs. This isn’t perfect but, we will measure this as the sum of the three input costs that we have:
gen tc=pay+invest+energy
We will model total cost as a cubic function of output. Thus we must generate the squared and cubed elements of the polynomial:
gen vadd_2=vadd^2
gen vadd_3=vadd^3
and then estimate the cost function:
reg tc vadd vadd_2 vadd_3, noc
Note the use of the noc (no constant) option. This forces the intercept term to equal zero.
a) What is the economic interpretation of suppressing the constant term (forcing it equal zero)? Why does that make sense to do here?
b) prepare out the cost function as:
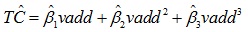
(Use the numbers from the regression you just ran.)
c) Now use your regression of TC to create predicted values of the average cost function and the marginal cost function.
Here’s how you do this in STATA. For average cost this is straight forward.
predict tcpred (This predicts the total cost for each level of vadd)
gen ac=tcpred/vadd
For marginal cost you need to issue the command
gen mc=a+2*b*vadd+3*c*vadd^2
(Where a, b, and c are beta values you have taken from your TC function of part 2.)
[Note: Why is this the marginal cost? Calculus. We have taken the derivative of tc with respect to vadd, and the above formula is the result.]
Report these equations.
Now we are going to graph the marginal and average cost functions.
sort vadd
scatter ac mc vadd, connect(l l)
The sort command lines the data up in the right order so that the graphs look nice. The scatter command will put ac and mc on the vertical axis and output (vadd) on the horizontal, just like in the textbooks, and the connect option will connect the dots (the l l stands for connecting with unbroken lines.)
d) Print out this graph. Does it look like the textbook depiction of average and marginal cost? Why or why not? That is, did your slope coefficients you estimated above conform to expectations?
C) Estimate the production function:
In this section you will estimate a Cobb-Douglas production function, where the log of output is a function of the log of inputs (and time).
Generate log versions of the output variable and the three inputs. For ex:
gen lvadd=log(vadd) and do the same for pay, invest and material.
Run a regression of lvadd on the three log input variables, and year. Test the hypotheses that:
a) the individual coefficient on each of the inputs =0. Rejection implies that the input is productive.
b) the individual coefficient on each of the inputs =1. Rejection in the direction <1 implies diminishing marginal productivity of the input.
c) the sum of the input coefficients=1. You may either do this with a by-hand F-test or use STATA’s test command (which is itself an F-test), and it’s even possible to do this with a t-test, if you really want to try. Rejection implies either increasing or decreasing returns to scale.
d) the coefficient of year =0. (Rejection (in the positive direction) implies technical progress is being made).
e) Broadly do you think this production function conforms to the ideas of economic theory?